逆旅，行人

这个题目困惑了本人很久，想过各种方法。不是因为脑容量不够而导致处理问题的栈不足而放弃，或者就是根本对上述的想法非常质疑，而又找不到更好的方法以致陷入不断的困惑中。最后还是一番google，找到了问题的解决方法，之所以要记下来，是因为在这道题上我又学习了一种新的解决问题的方法。我姑且称之为“归纳法” + “倒推法”。

题目是这样的: Starting in the top left corner of a 22 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 2020 grid?

解决方法是从程序的出口，即最右下角入手进行倒推。首先要想到达最右下角那个点，只有两个点可以到达，即紧挨着的它上面和它左边的那个点。

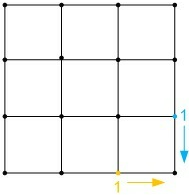
同时我们可以看到，正方形的最右和最下这两个边上的除了终点的所有点到达终点的方式都只有一种，所以可以把它们全部赋值为1。 紧接着，我们可以继续向前推，到达与终点斜对角的第一个点。这个点到达终点无外乎两种方式，即通过它右边的那个点或者它下边的那个点到达。所以它到达终点（为了下文叙述方便，姑且称其为A点）共有2种方式。 接着，我们继续刚才的推导过程。A点左边那个点到达终点的方式=A点到达终点的方式+A点右边那个点下面那个点到达终点的方式。所以它一共有3种方式到达终点。

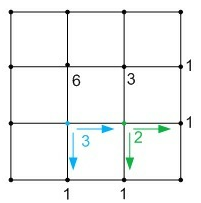
这样我们一直向回推导，就能推导最左上角到达终点的方式=它下面的那个点到达终点的方式+它右边的那个点到达终点的方式。 最后，程序代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

package problems;

public class Problem_15 {
    public static void main(String[] args) {
        long[][] paths = new long[21][21];

        // initialize the boundries
        for (int i = 0; i < 20; i++) {
            paths[i][20] = 1;
            paths[20][i] = 1;
        }

        for (int i = 19; i >= 0; i--) {
            for (int j = 19; j >= 0; j--) {
                paths[i][j] = paths[i + 1][j] + paths[i][j + 1];
            }
        }

        System.out.println(paths[0][0]);
    }
}