逆旅，行人

一、选择排序

选择排序之所以被称为选择排序是因为在每一次的迭代过程中，总是‘选择’最小的一个元素到数组的最左边。下面是一个选择排序的实例：

1
2
3
4
5
6
7
8
9
10
11
12

private static void sort(String[] a) {
    int N = a.length;
    for (int i = 0; i < N; i++) {
        int min = i;
        for (int j = i + 1; j < N; j++) {
            if (a[j] < a[min]) {
                min = j;
            }
        }
        exchange(i, min);
    }
}

我们可以通过下面这个图来直观地看到排序的过程和结果：

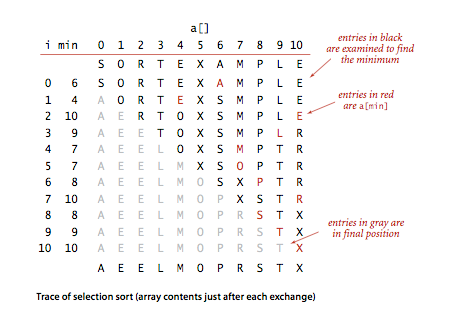
此算法一共执行(N-1) + (N-2) + … + 2 + 1 + 0 ~ N²(N的平方)次比较(if语句)，N次顺序调换(执行exchange的次数)。这个算法不好的地方在于它对于混乱的或者已经排好序的数组一视同仁，一个已经排好序的数组的执行时间并不会和混乱的数组的执行时间有什么差别。

二、插入排序 & 希尔排序

1、插入排序 插入排序是一种通过不断地把新元素插入到已排好序的数据中的排序算法，常用的插入排序算法包括直接插入排序和shell排序，直接插入排序实现比较简单，下面是插入排序的实例：

1
2
3
4
5
6
7
8
9

private static void sort(String[] a) {
    int N = a.length;
    for (int i = 1; i < N; i++) {
        for (int j = i; j > 0 && (a[j] < a[j-1]); j--) {
        // for循环的第二个条件一旦不成立就会跳出循环，所以如果遇到12345，3 >  2会跳出循环，并且i加1
          exchange(j, j-1);
        }
    }
}

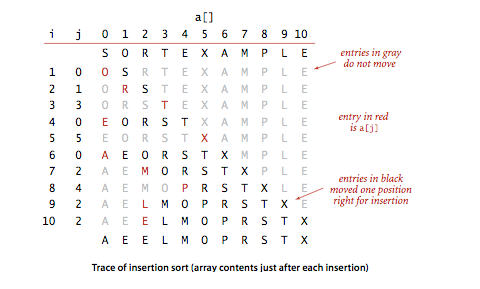
对插入排序来说，最坏的情况是所有的数组反序排列。这种情况下，内层for循环中的比较语句一共被执行的次数是1 + 2 + … + (N-2) + (N-1)N²(N的平方)次，exchange也被执行这么多次。最好的情况是数组顺序排列，这种情况下，内层for循环中的比较语句一共被执行N-1此，exchange被执行0次。平均下来插入排序使用~N²/4次比较和同样多次数的exchange。

选择排序无论怎么样都会被执行N²次，而插入排序最坏的情况才这么多，这就是插入排序通常比选择排序快的原因。

2、希尔排序 另一种常用的插入排序算法：Shell排序也是对直接插入排序算法的一种优化，因此可以说直接插入排序是一种特殊的Shell排序，Shell排序对直接插入排序的优化主要体现在，Shell排序通过使用一个增量序列（递减），每次把要排序的数组分成几个子数组，然后对子数组进行插入排序，这样可以减少比较和移动数据的次数，Shell排序是一种非常高效的排序算法，该算法的思想是：

2.1.以h（h一般取n/2）为间隔将n个元素列分为几个小组，在每个小组内按直接插入法排序

2.2.令h=h/2，重复第1步

2.3.当h=1时，排序结束（此时相当于直接插入排序，不过由于数据已经基本排好序，因此比较次数和移动次数比直接插入排序少很多）Shell排序的Java实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

private static void sort(String[] a) {
    int N = a.length;
    int h = 1;
    while (h < N / 3) {
        h = h * 3 + 1; // 1, 4, 13, 40, 121 ...
    }

    while (h > 0) {
        for (int i = h; i < N; i++) {
            int j = i;
            while ((j > 0) && a[j] < a[j - h]) {
                exchange(j, j - h);
                j--;
            }
        }
        h /= 3;
    }
}

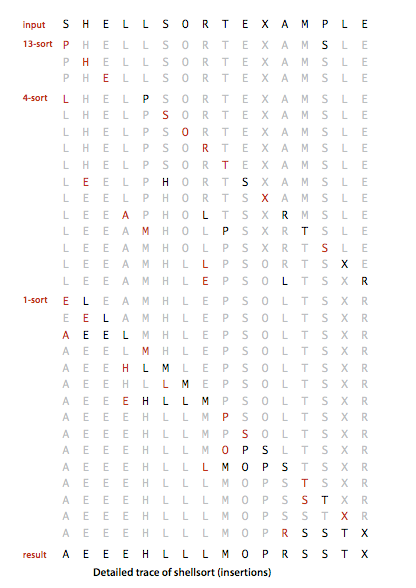
希尔排序比选择和插入排序都快，且随着输入的增大体现尤为明显。