逆旅，行人

Merge sort即归并排序，它的中心思想是分而治之(divide and conquer)，即将一个原来很大的待排序数列分成若干个小的数列然后分别对他们进行排序，最后把小的排好序的数列合并起来。这个过程可以分为三个步骤：

第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.

第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作。

第三, 合并: 合并两个排好序的子序列,生成排序结果。

在我看来，归并排序中最重要的还是‘合并’，因为在多次递归分解之后，剩下的大小为2的数组都是通过‘合并’过程达到排序的目的。合并的过程很简单，从下面这张图就能大概看出来：

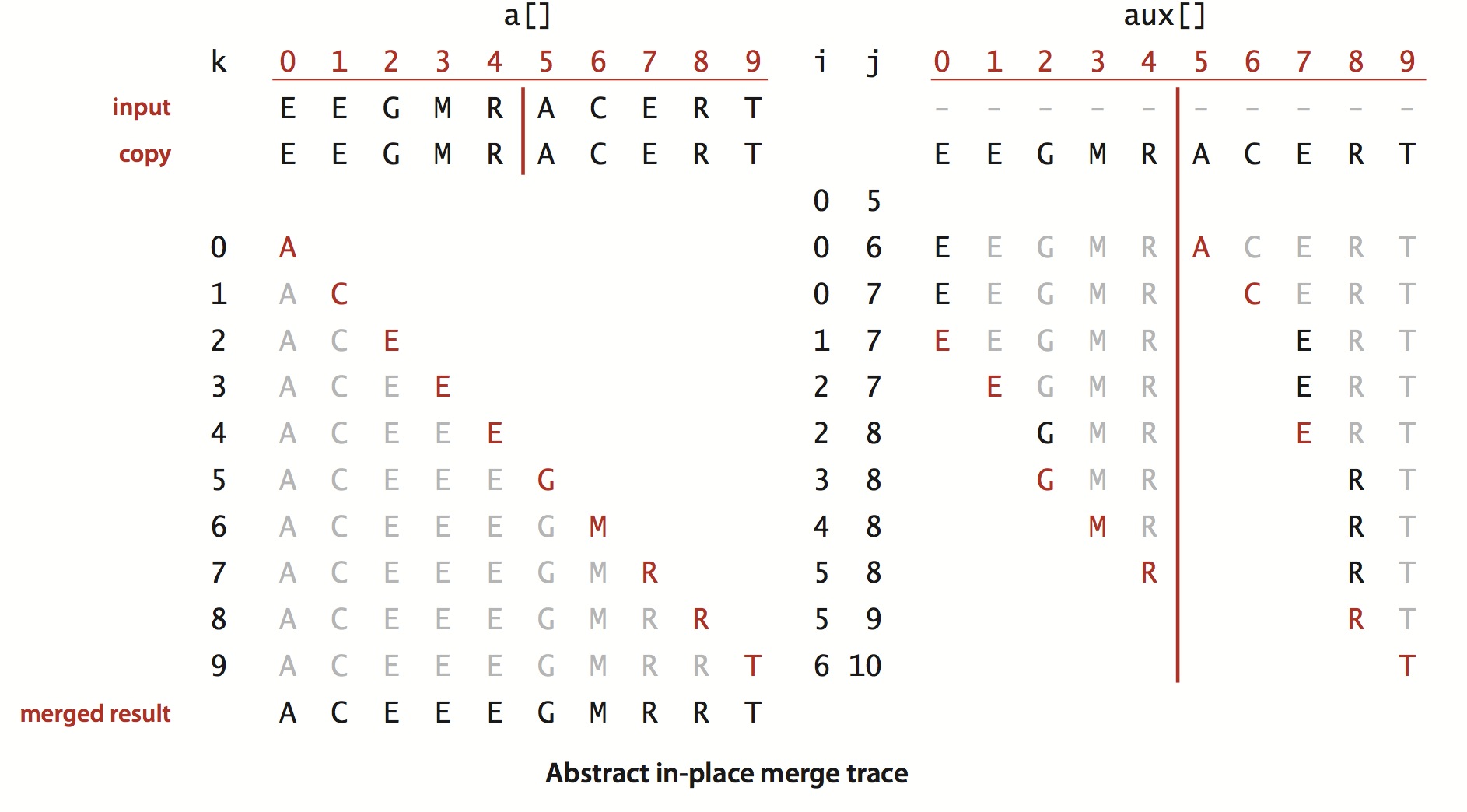
对于一个数组来说，有low、mid和high三个位置，有两个指针分别从low和mid+1的位置开始后移，在升序的情况下，取low和mid+1中小的值并将其自加，直到数列被统计完为止。这个过程的代码描述如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

public static void merge(int[] a, int low, int mid, int high) {
    int i = low, j = mid + 1;

    System.arraycopy(a, low, aux, low, high + 1 - low);

    for (int k = low; k <= high; k++) {
        if (i > mid) {
            a[k] = aux[j++];
        } else if (j > high) {
            a[k] = aux[i++];
        } else if (aux[i] > aux[j]) {
            a[k] = aux[j++];
        } else if (aux[i] < aux[j]) {
            a[k] = aux[i++];
        } else if (aux[i] == aux[j]) {
            a[k++] = aux[i++];
            a[k] = aux[j++];
        }
    }
}

System.arraycopy是将a中的数据拷贝到aux(辅助数列)中，如果i大于mid，说明mid前面的数据已经用完了，就将mid+1后面没有用完的数依次放到a中，同理可解释j大于high的情况。然后就是三种不同的情况下的处理。

我们之所以说排序过程是在merge中做的是因为第一个被merge的数组必定是low=0，mid=0，high=1的一个长度为2的数组，我们可以通过merge把他排序，当下一次处理长度为3的数组时，由于前两个数字已经排好序，所以merge方法同样可以排序它，进而对长度更大的数组同样有效，这其实是一个递归的过程。那么下面我们就来看看应用merge的方法吧–sort。

Sort其实是一个递归的过程，它不断将大的数组分成小的数组然后分别对他们应用merge，代码如下：

1
2
3
4
5
6
7
8

public static void sort(int[] a, int low, int high) {
    if (low >= high)
        return;
    int mid = low + (high - low) / 2;
    sort(a, low, mid);
    sort(a, mid + 1, high);
    merge(a, low, mid, high);
}

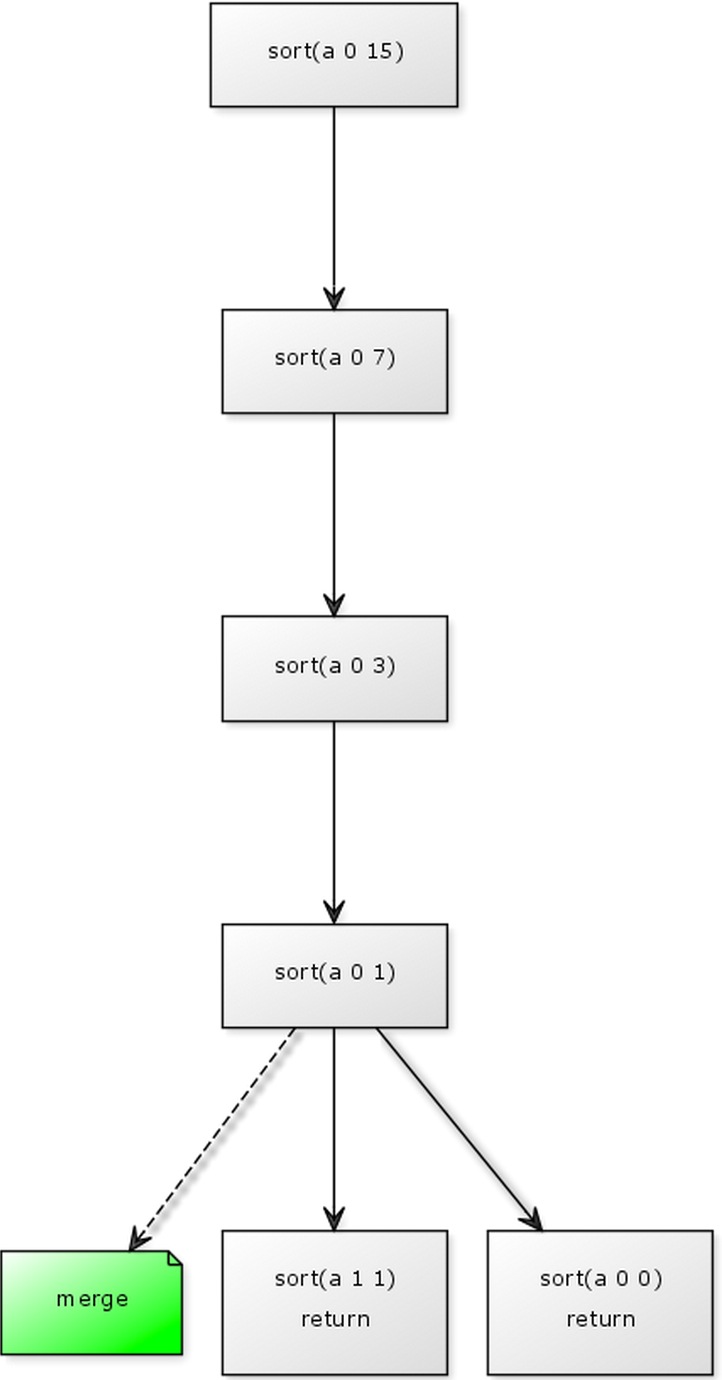
这里的递归让我迷惑了很久，所以还是很有必要记录下这个递归的过程。就拿一个长度为15的数组来举例吧，它在第一次递归到最后是下面这种情况：

第2次

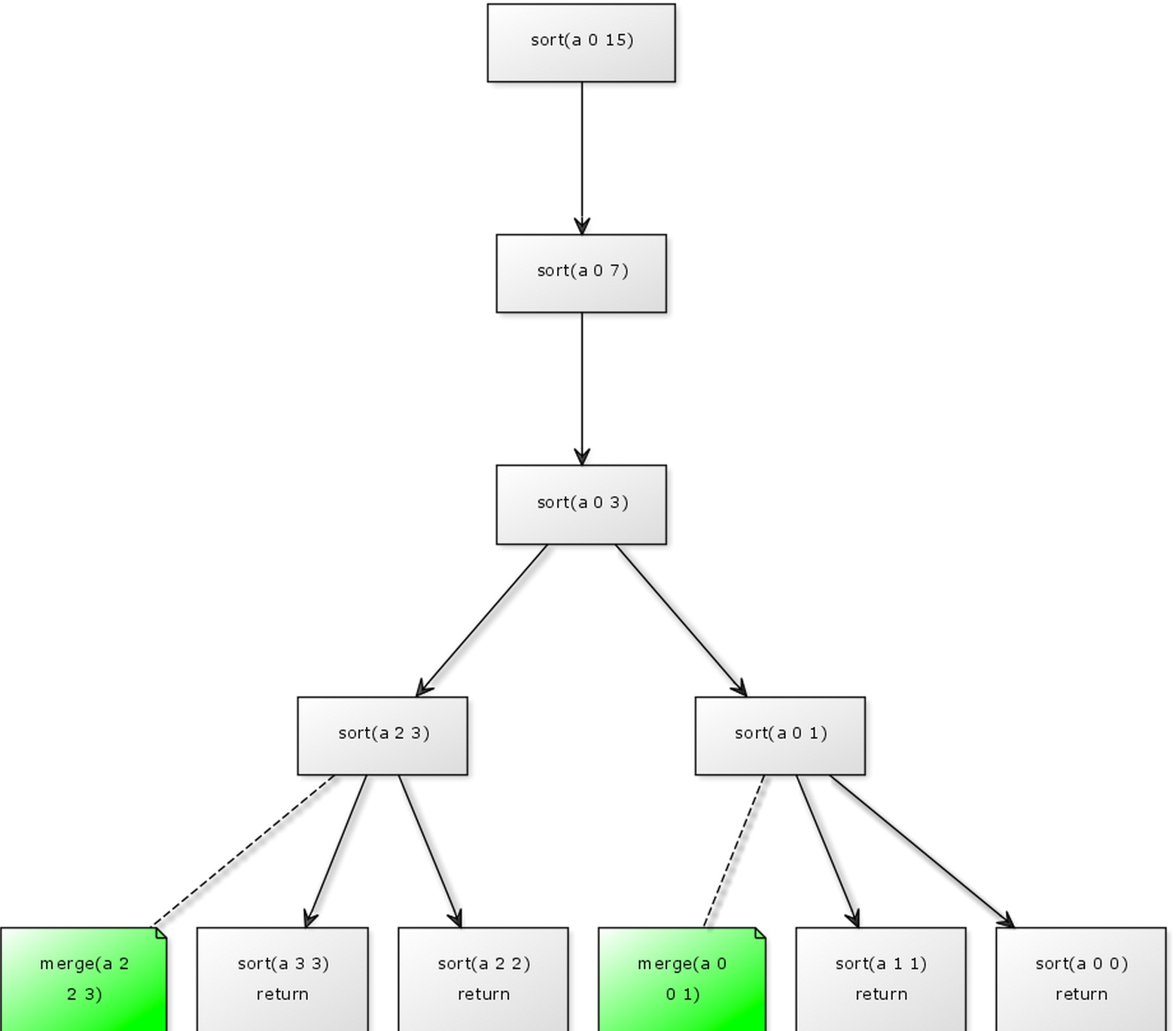
第3次

第4次

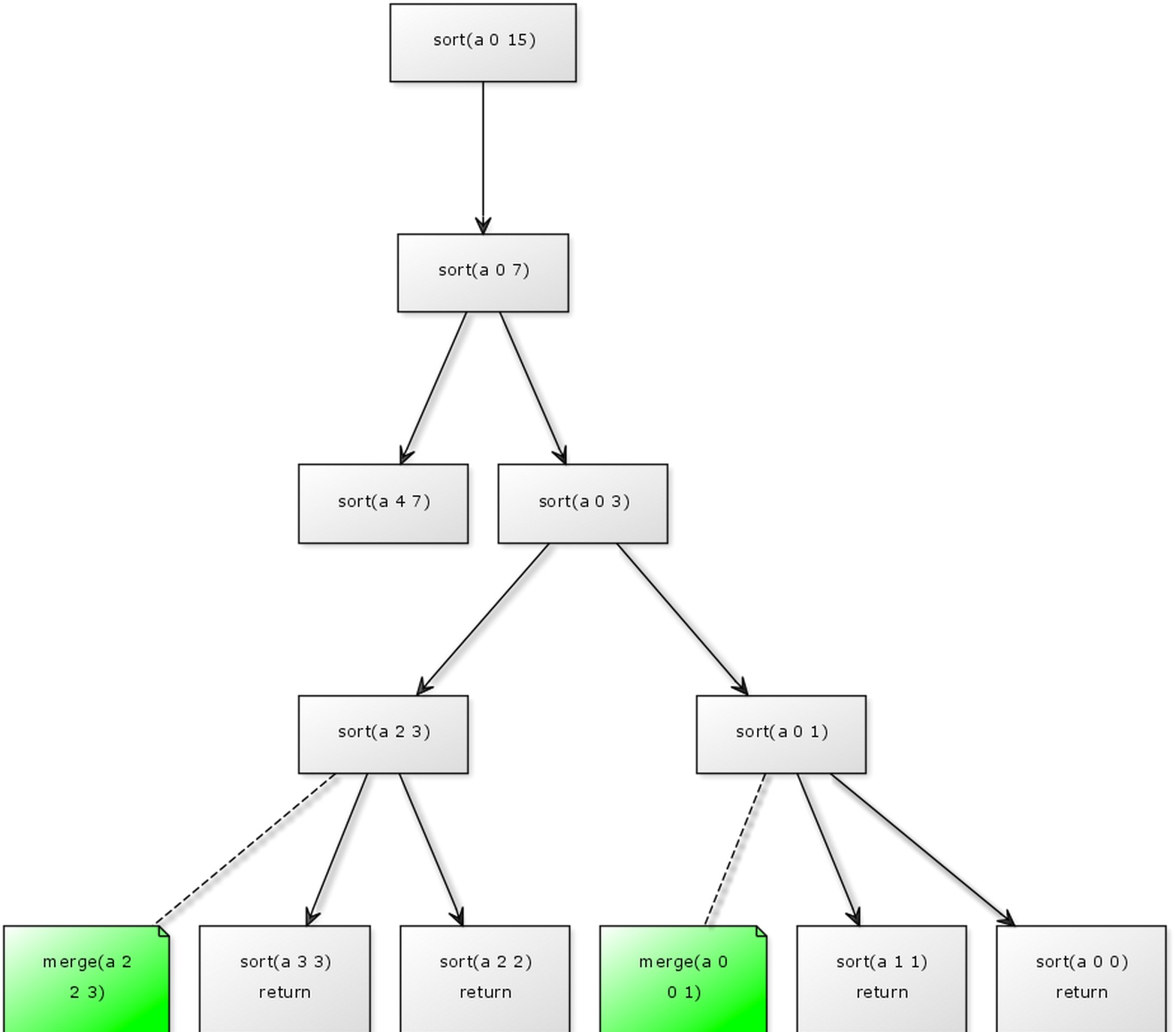
后面的以此类推

上面就是sort在递归中对每一个小分支执行merge算法的过程。